Новосибирск, «Наука», 1979
Г лава 4
УЧЕТ В СЕТЕВЫХ МОДЕЛЯХ ВЕРОЯТНОСТНО-НЕОПРЕДЕЛЕННЫХ СВОЙСТВ РАЗВИТИЯ ОТРАСЛЕВЫХ СИСТЕМ
1. О ВЛИЯНИИ СТОХАСТИЧЕСКИХ ФАКТОРОВ НА РАЗВИТИЕ ОТРАСЛЕЙ НАРОДНОГО ХОЗЯЙСТВА
Современные отрасли хозяйства характеризуются в первую очередь организационной сложностью, наличием многочисленных внешних и внутренних связей, динамичностью и ярко выраженным вероятностным характером функционирования. Процессы развития и размещения объектов различных отраслей народного хозяйства протекают под воздействием комплекса внешних н внутренних случайных факторов.
К внутренним относятся случайные факторы отраслевого характера: надежность функционирования различных объектов отрасли, периоды вывода сооружаемых и реконструируемых объектов на проектную мощность, темпы технического прогресса в данной отрасли народного хозяйства и т. д.
Внешние факторы определяются взаимодействием рассматриваемой отрасли с сопряженными отраслями народного хозяйства. Это темпы развития народного хозяйства, выделяемые капитальные вложения, лимитированные виды продукции сопряженных отраслей, сроки сдачи сооружаемых и реконструируемых объектов отрасли, технический прогресс в сопряженных отраслях народного хозяйства и т.д.
Кроме того, к внешним должны быть отнесены случайные факторы, обусловленные взаимодействием с природной средой. Для добывающих отраслей народного хозяйства основными из них являются открытие новых месторождений полезных ископаемых и корректировка запасов полезных ископаемых на эксплуатируемых месторождениях [51].
Неадаптируемость и детерминизм большинства моделей, используемых при перспективном планировании развития и размещения объектов отдельных отраслей народного хозяйства или отраслевых систем, делают их весьма неустойчивыми и неадекватными по отношению к неизбежным изменениям моделируемых систем, происходящих под воздействием комплекса случайных факторов. Для обеспечения допустимой степени соответствия используемых моделей моделируемым процессам часто требуются значительные затраты труда высококвалифицированных специалистов.
Например, в строительном производстве такие показатели и факторы, как продолжительность, трудоемкость, сметная стоимость, сроки и объемы поставок различных материалов и оборудования являются вероятностными в силу воздействия на них множества случайных факторов. Естественно, что это должно учитываться, хотя и в различной степени, при составлении перспективных, текущих и оперативных планов сооружения комплексов различных объектов.
Очевидно, что учет при перспективном планировании отраслевых систем вероятностно-неопределенных свойств их развития обусловит повышение степени адекватности комплекса применяемых экопомико-математических моделей реальным процессам развития и размещения объектов отраслевых систем.
В вероятностном и статистическом представлении изучаемых объектов состоит одна из основных концепций современного мировоззрения. При этом схемы жесткой детерминации рассматриваются как частные предельные случаи. Вероятностный подход оказался весьма плодотворным при создании теории надежности, базирующейся в основном на понятиях и методах теории вероятности.
Надежность — вероятностная категория, присущая как техническим, так и более сложным организационно-технологическим системам, включающим экономические и социальные аспекты. В настоящее время наибольшие успехи достигнуты в изучении надежности технических систем. Об этом свидетельствует создание высоконадежных сложнейших технических устройств, таких как ЭВМ, космические системы.
Введение понятия надежности перспективных планов развития отраслевых систем во многом стимулировано результатами, полученными при исследовании надежности технических и биологических систем [52, 15]. При этом, конечно, следует учитывать, что полной аналогии между понятиями надежности технической системы и потенциальной надежности перспективных планов нет. Так, например, надежность технической системы может быть сколь угодно близкой к единице, но не будет равняться единице. В то же время допустимо положить, что надежность перспективного плана принимает значения больше единицы в случае превышения фактических показателей над теми, которые были запланированы в исходном варианте плана.
При формировании понятия потенциальной надежности планов термин «надежность» применяется в дальнейшем только лишь к результату деятельности системы. Исследование проблемы надежности для многих систем показывает, что надежность результата, как правило, достигается за счет перестройки системы, гибкости и пластичности, т. е. ненадежности самой системы, понимаемой как жесткая детерминированная схема. Естественно, что определение надежности в терминах получения необходимого результата предполагает возможность в экстремальных ситуациях структурной перестройки системы и функциональной замены отказавших элементов другими, которые ранее могли выполнять иные функции.
Как известно, основное направление повышения надежности технических систем принципиально иное: механическое дублирование и резервирование элементов — построение надежных систем из ненадежных элементов. В этом отношении технические системы могут рассматриваться как антиподы биологических, для которых свойственно минимальное дублирование и резервирование при максимальной адаптивности.
Учет в моделях оптимального перспективного планирования вероятностно-неопределенных свойств развития отраслевых систем служит повышению надежности применяемых вариантов перспективных планов. В настоящее время в Институте экономики и организации промышленного производства СО АН СССР разрабатываются два направления учета в комплексе моделей перспективного планирования вероятностно-неопределенных свойств развития экономических систем. Первое направление связано с развитием и совершенствованием аппарата стохастического программирования, в частности с разработкой многоуровневых стохастических систем моделей. Второе направление, некоторые аспекты которого будут освещены ниже, связано с определением и отражением в моделях адаптивных характеристик планов [53].
Необходимо отметить, что хотя в настоящее время имеется достаточно разработанный и апробированный аппарат стохастического программирования, однако эффективность его использования в оптимальном перспективном планировании ограничивается рядом факторов. Укажем основные из них:
- размерность большинства задач перспективного планирования развития и размещения отраслей промышленности или развития межотраслевых программных комплексов превосходит вычислительные возможности алгоритмов стохастического программирования;
- большинство алгоритмов для решения задач стохастического программирования требует такого информационного обеспечения, подготовка которого трудоемка и затруднительна;
- в известных моделях стохастического программирования учитываются вероятностные свойства параметров модели, структура же модели остается детерминированной;
- использование аппарата стохастического программирования в значительной степени исключает возможность применения полученных ранее результатов по созданию отраслевого алгоритмического обеспечения так как требует нового определения таких основных понятий, как область допустимых решений, целевая функция и т.д.
Использование адаптивных характеристик в оптимальном перспективном планировании следует рассматривать как попытку анализа некоторых вероятностных аспектов развития сложных экономических систем в рамках детерминированного экономико-математического аппарата.
2. АНАЛИЗ МАНЕВРЕННЫХ ХАРАКТЕРИСТИК
ПЕРСПЕКТИВНЫХ ПЛАНОВ
Возможны различные подходы к использованию многоуровневых сетевых моделей для анализа ряда вероятностно-неопределенных аспектов планов. Одни из них состоит и учете адаптивных характеристик перспективного плана как дополнительных ресурсных ограничений. Принципиально такой подход может быть реализован и при использовании несетевых оптимизационных моделей отраслевого планирования: линейных [53], нелинейных, целочисленных. В настоящем параграфе рассматривается использование характеристик маневренности перспективных планов при реализации многоуровневых сетевых моделей оптимизации развития отраслевых систем. Анализ различных топологических характеристик ресурсной сетевой модели, таких как, например, категорийность событий и узлов или иерархичность фронтов работ, описанных в гл. 1, может проводиться с точки зрения их влияния на адаптивные характеристики перспективных планов. Ниже будут использованы понятия топологической, временной и ресурсно обусловленной иерархичности фронтов работ.
В настоящее время получены первые результаты по анализу адаптивных характеристик планов с помощью линейных и сетевых моделей [53]. Естественно, применение сетевых подходов не ставит целью дублирование результатов, полученных с помощью линейно-программных моделей. Да это было бы и крайне затруднительно, если учитывать существенную разницу между линейными и сетевыми оптимизационными моделями. Анализ адаптивных характеристик перспективных планов с помощью сетевых моделей позволяет получить некоторые новые представления об этих категориях.
Маневренность плана характеризуется возможной предельной скоростью его изменений (ускорением) во времени. Маневрирование рассматривается как реакция системы (плана) на изменение внешних и внутренних условий реализации плана, а также самих целевых установок плана [53]. Введению некоторых определений маневренных качеств перспективных планов целесообразно предпослать следующее замечание. Ресурсно обусловленная иерархичность фронтов работ сетевых моделей различных уровней может быть использована не только для анализа маневренности и других адаптивных характеристик, но в дальнейшем и в качестве эффективного инструмента управления как собственно маневренными свойствами перспективных планов, так и какой-либо комплексной адаптивной характеристикой (например, потенциальной адаптивностью), включающей в себя одним из элементов и маневренность.
Назовем оптимальный перспективный план, составленный для рассматриваемого планируемого периода времени [0, Т], исходным. Пусть в какой-то момент t* планируемого периода (0<t*<T) произойдут изменения внутренних или внешних условий функционирования исходного плана (или, в общем случае, изменение комплекса как внешних, так и внутренних условий). Тогда может быть составлен новый вариант оптимального перспективного плана, который назовем вторичным. При использовании многоуровневых сетевых моделей как исходный, так и вторичный оптимальные перспективные планы будут определяться ресурсно обусловленной иерархичностью фронтов работ.
Назовем планируемую систему абсолютно инерционной, если у исходного и произвольного вторичного оптимальных планов совпадают не только составы соответствующих фронтов работ, но и их продолжительности, а также все параметры, характеризующие работы этих сетевых моделей.
Будем считать планируемую систему условно инерционной, если составы соответствующих фронтов работ совпадают, но продолжительности отдельных совпадающих по составу фронтов работ могут отличаться.
И наконец, планируемая система считается условно-маневренной, если различаются составы некоторых соответствующих фронтов работ для исходного и вторичного оптимальных планов.
Естественно, что приведенные выше три определения маневренности качеств планируемой системы подразумевают совпадение базисов исходного I1 и вторичного I2 оптимальных планов (отметим, что базис оптимального плана определяется как совокупность объектов с ненулевыми компонентами интенсивностей, включенных в оптимальный план).
Таким образом, использование понятия ресурсно обусловленной иерархичности фронтов работ сетевых моделей позволяет расширить и уточнить понятие абсолютной инерционности планируемой системы, предложенное при использовании линейных оптимизационных моделей. Так, например, базисы исходного и вторичного оптимальных планов могут совпадать, однако при этом возможно существенное изменение сроков ввода отдельных сооружаемых или реконструируемых объектов, попавших в базис оптимального плана. А этот фактор имеет существенное значение с точки зрения связей рассматриваемой отрасли с сопряженными отраслями народного хозяйства.
Планируемая система будет абсолютно маневренной, если выполняется условие
I1 ⋂ I2 = Ø. (4.1)
И абсолютная инерционность планируемой системы, и ее абсолютная маневренность должны рассматриваться как некие экстремальные ситуации, которые крайне редко возникают при оптимизации перспективных планов. Наиболее же распространена ситуация, при которой
F = I1 ⋂ I2 ≠ Ø. (4.2)
Множество F состоит из объектов, которые попадают как в исходный, так и во вторичный оптимальные планы. Это множество объектов, которое в дальнейшем будем называть ядром инерционности оптимального плана, в некоторой степени характеризует маневренные качества планируемой системы. Однако само по себе оно не дает еще сколько-нибудь исчерпывающей информации о маневренности оптимального перспективного плана. Отметим, что одно и то же число объектов может составлять различный удельный вес в оптимальном плане как по затратам и выпуску планируемой продукции, так и по необходимым для сооружения или реконструкции этих объектов ресурсам различных категорий.
Введем понятие интегральной маневренности оптимального перспективного плана. Необходимо сразу же оговорить то обстоятельство, то принципиально возможно введение различных понятий интегральной маневренности. Они могут различаться как по отражению различных аспектов маневренных качеств перспективных планов, так и по степени содержательности отражения какого-либо изучаемого аспекта маневренности.
Предлагаемое понятие интегральной маневренности перспективного плана должно рассматриваться лишь как некоторая многофакторная характеристика ядра инерционности. Приведем ряд определений и обозначений, которые потребуются для формулировки понятия интегральной маневренности. Верхние индексы I1, I2 и F в употребляющихся в дельнейшем обозначениях будут свидетельствовать о принадлежности соответствующего параметра исходному оптимальному плану, вторичному оптимальному плану или ядру инерционности.
Ресурсно обусловленная иерархичность фронтов работ исходного и вторичного оптимальных планов будет связана с диаграммами распределения ресурсов DI1l (t) и DI2l соответственно (l= 1, 2, …, L). Неравенство
DI1l (t) ≠ DI2l (t), t* ≤ t ≤ T (4.3)
которое может выполняться для некоторых ресурсов, в общем случае обусловливается изменением внешних условий функционирования исходного плана, выражающимся в изменении объемов поставки l-го ресурса.
Интегральную меру маневренности предлагается характеризовать следующим комплексом показателей:
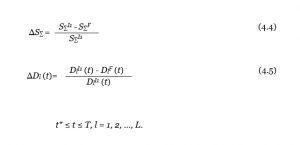
Абсолютно инерционная планируемая система может определяться как такая система, для которой выполняются условия
∆S∑ = ∆Dl (t) ≡ 0, l = 1, 2, …., L. (4.6)
Для условно инерционной и условно маневренной планируемых систем какое-либо из равенств (4.6) может не выполняться в связи с тем, что ресурсно обусловленные иерархичности фронтов работ исходного и вторичного оптимальных планов могут отличаться как продолжительностью, так и составами отдельных фронтов работ.
В общем случае величина ∆S∑ будет определять степень маневренности перспективного плана по затратной характеристике, а функция ∆Dl (t) характеризовать изменение в течение планируемого периода времени степени маневренности перспективного плана по l-му ресурсу.
Для абсолютно маневренной планируемой системы
∆S∑ = ∆Dl (t) ≡ 1, l = 1, 2, …., L. (4.7)
Отметим, что величины ∆S∑ и L функций ∆Dl (t) дают некоторую характеристику интегральной меры маневренности перспективного плана. Необходимо еще раз подчеркнуть, что это понятие связано только с ядром инерционности исходного оптимального плана. В общем случае вторичный оптимальный план будет характеризоваться своим комплексом параметров
S∑I2 и DlI2 (t) (l = 1, 2, . . ., L).
Интегральная мера маневренности, описываемая комплексом параметров ∆S∑ и ∆Dl (t), показывает «долю» исходного перспективного плана (характеризуемую относительными суммарными приведенными затратами и относительной потребностью в ресурсах), которая является маневренной.
Объекты из ядра инерционности могут характеризоваться различными параметрами (например, приведенными затратами с учетом фактора дисконтирования или потребностью в ресурсах) по исходному и вторичному оптимальным планам. Выше параметры объектов из ядра инерционности определялись по исходному перспективному плану.
Предложенные понятия иерархичности фронтов работ сетевой модели верхнего уровня могут быть использованы для введения и некоторых других определений интегральной меры маневренности перспективного плана. Так, например, интегральная мера маневренности может быть определена как множество допустимых выборов ωt* при изменении в момент t* условий функционирования исходного плана:
ωt* = Λ0t* \ (υ0)t* (4.8)
где — Λ0t* — множество начальных работ преобразованной ресурсной сетевой модели Ωt*, получающейся из исходной какого-либо уровня в результате реализации части исходного оптимального плана к моменту времени t*;
(υ0)t* —подмножество работ из Λ0t*, выполнение которых безусловно обязательно в связи с реализацией части оптимального базиса исходного плана.
3. АНАЛИЗ ПОТЕНЦИАЛЬНОЙ АДАПТИВНОСТИ
ПЕРСПЕКТИВНЫХ ПЛАНОВ
Приведенные в гл. 1 определения сложного события и узла сетевой модели используем для анализа потенциальной адаптивности перспективных планов развития отраслевых систем. Отметим лишь, что эти определения основываются на анализе топологической структуры сети и не зависят от временных, ресурсных или стоимостных характеристик работ рассматриваемого сетевого графика Ω .
Потенциальная адаптивность плана определяется как способность исходного плана, рассчитанного на определенные внешние и внутренние условия, безболезненно (без дополнительных затрат или при непревышении определенного уровня затрат) приспосабливаться к возникающим новым (как правило, непредусмотренным или вероятностным) условиям [53].
Адаптивные качества планов служат их важнейшей характеристикой при наличии неопределенности или вероятностного характера в будущих условиях реализации этих планов. Причем более адаптивные варианты перспективных планов развития межотраслевых программных комплексов должны получать определенные преимущества.
В работе [18] предложено различия адаптивных качеств вариантов перспективных планов, обусловленные различиями в динамике затрат, характеризовать через момент затрат, определяемый по аналогии со вторым моментом сил в механике. Момент затрат — это сумма произведений затрат каждого Θ-го года планируемого периода (приведенных по фактору времени) на квадрат плеча этих затрат, т. е. на число Θ2:
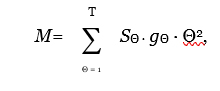(4.9)
где M — момент затрат;
SΘ — затраты Θ-го года;
gΘ = (1 +E)—Θ — коэффициент дисконтирования, учитывающий различную значимость затрат, осуществляемых в разные годы;
Е — коэффициент эффективности.
Момент затрат может рассматриваться как одна из мер адаптивности перспективного плана. Весьма полезно использовать этот показатель в качестве дополнительного критерия при анализе множества вариантов плана, находящихся в зоне экономической неопределенности при оптимизации по основному критерию (например, по критерию минимума суммарных затрат с учетом фактора времени) [54].
Необходимо отметить, что целесообразность введения меры адаптивности плана связана с неопределенностью и вероятностной природой некоторых из предстоящих условий реализации плана. Подобная ситуация наиболее характерна для процедур перспективного планирования и прогнозирования.
При использовании многоуровневых сетевых моделей для оптимизации перспективных планов развития и размещения отраслевых систем момент затрат может быть определен таким образом:
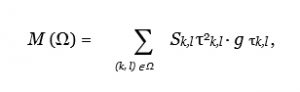(4.10)
где Sk,l — затраты на выполнения работы (k, l)
τk,l — начало работы (k, l)
Момент затрат перспективного плана, определяемый соотношением (4.10), является функцией времени начала работ соответствующей сетевой модели. Верхнюю и нижнюю границы изменения M (Ω) определим так:
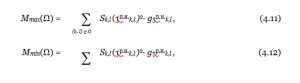
где τр.н.k,l — раннее начало работы (k, l);
τп.н.k,l – позднее начало этой же работы.
Определения меры адаптивности перспективных планов (4.9) или (4.10) выбраны таким образом, чтобы вариантам плана, характеризующимся большей степенью адаптивности, соответствовало и большее значение меры адаптивности.
Функция
f (t) = t2gt
монотонно возрастает (при E≤0,12), если t ≤ 17. В связи с этим предложенное определение меры адаптивности может быть использовано для анализа вариантов плана, составленных на 10—15-летнюю перспективу. Указанным фактором и объясняется то обстоятельство, что момент затрат (4.9) или (4.10) является аналогом второго, а не первого момента сил в механике.
Для анализа адаптивных характеристик вариантов перспективных планов используем предложенные в гл. 1 определения узла и области влияния произвольного сложного события (в том числе и узла). Рассмотрим произвольный i-й узел первой категории с областью влияния [i, z(i)]. Пусть ni — число работ, начальным событием которых является i. Будем говорить, что область влияния i-го узла состоит из ni путей. Через tβ обозначим длину β-го пути (от события i до события z(i), входящего в область влияния i—го узла первой категории (1≤β≤ni). Кроме того, через ñi обозначим число путей немаксимальной длины, входящих в область влияния i-го узла первой категории.
В общем случае
0≤i≤ni -1
Вели i + 1= ni, то области влияния [i, z(i)] будет принадлежать единственный путь максимальной длины. Если же i =0, то все пути, принадлежащие области влияния [i, z(i)], имеют одинаковую длину.
Минимальным моментом затрат i-го узла первой категории будем считать величину
Запас момента затрат i-го узла первой категории ∆M(i) может рассчитываться по формуле:
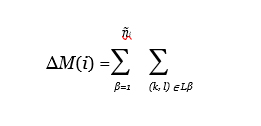
где — Lβ множество работ пути с номером β, принадлежащего области влияния i-го узла;
∆τβ — разность длин максимального и произвольного β-го пути.
Необходимо отметить, что условие ∆M(i) =0 не обозначает совпадения моментов затрат по различным путям, образующим область влияния i-го узла.
Если вычислены по формулам (4.14) — (4.16) минимальный и максимальный моменты затрат и запас момента затрат для всех узлов первой категории, то эти величины могут быть определены и для узлов второй категории. При этом узлы первой категории интерпретируются как обобщенные работы с моментами затрат вычисленными по (4.15). Таким образом и сами узлы второй категории будут интерпретироваться как обобщенные узлы первой категории. Расчет минимального и максимального моментов затрат, а также запаса момента затрат (при сделанной оговорке) для узлов второй категории также может производиться по формулам (4.14)—(4.16).
Аналогично, если вычислены моменты затрат для узлов (n-1)-й категории, то эти узлы могут интерпретироваться как обобщенные работы, принадлежащие областям влияния узлов n-й категории, а сами узлы n-й категории (в данной ситуации) —как обобщенные узлы первой категории. Тогда для определения моментов затрат могут быть использованы формулы (4.14) — (4.16).
Предложенные определения минимального и максимального моментов затрат, а также запаса момента затрат модифицируются и для областей влияния сложных событий произвольной категории. Но в этом случае значительно усложняется процедура вычисления максимального момента затрат и запаса момента затрат. Так как области влияния различных сложных событий могут пересекаться, то вычисления названных величин уже нельзя проводить локально для сложных событий произвольной (n—1)-й категории, а затем рассматривать область влияния этих сложных событий как обобщенные работы, принадлежащие областям влияния сложных событий n-й категории.
Как уже отмечалось, понятие момента затрат, принимаемое в качестве меры адаптивности вариантов перспективных планов, может быть использовано в качестве дополнительного критерия при отборе вариантов плана, находящихся в зоне экономической неопределенности. Так, например, из зоны экономической неопределенности, имеющейся при оптимизации по основному критерию, может быть выбрано подмножество вариантов ω с наибольшими значениями минимальных моментов затрат, вычисляемых по формуле (4.12). Здесь представляется целесообразным сделать одно замечание о выборе величин τр.н.k,l. Их определение обуславливается в основном типом используемой при оптимизации перспективного плана сетевой модели. Если необходимые для реализации плана ресурсы учитываются лишь при исчислении величин Sk,l и работы сетевой оптимизационной модели характеризуются только временными и стоимостными параметрами, то значения τр.н.k,l могут вычисляться на основе временной иерархичности фронтов работ. Если же работы сетевой оптимизационной модели кроме временной и стоимостной имеют еще и ресурсные характеристики, то величины τр.н.k,l будут определяться на основании ресурсно обусловленной иерархичности фронтов работ.
Комплекс основных факторов, обусловливающих наличие зоны экономической неопределенности при оптимизации перспективных планов развития и размещення отраслей промышленности, будет формировать и зону экономической неопределенности при вычислении моментов затрат, характеризующих различные варианты плана. Возможны два пути дополнительного выбора подмножества вариантов (в частности, может состоять из одного варианта) из отобранного по предложенному дополнительному критерию множества вариантов ω. Во-первых, в подмножество отбираются варианты с наибольшими значениями максимальных моментов затрат, вычисляемых по формуле (4.15). Во-вторых, для этих целей используются результаты анализа локальных запасов моментов затрат, рассчитанных по формуле (4.16). Причем в подмножество отбираются варианты с максимальными суммарными запасами моментов затрат по тем узлам произвольных категорий,
для ближайших замыканий которых выполняется условие
τр.н.z(i) ≤ (4.17)
где τр.н.z(i) — время раннего начала событпя z(i), являющегося ближайшим замыканием i-го узла;
— выделенный начальный интервал планируемого периода времени (0<<T).
Второй способ формирования подмножества вариантов перспективного плана позволяет повышать и маневренные качества плана.
Таким образом, введенные в гл. I определения узла сетевой модели и области его влияния могут быть использованы при формировании вспомогательного критерия выделения вариантов перспективных планов из зоны экономической неопределенности.
Возможны и другие подходы к использованию этих понятий при исследовании потенциальной адаптивности перспективных планов. Так, например, понятие области влияния узла произвольной категории может служить инструментом для выделения адаптируемой и неадаптируемой частей перспективного плана при возможных изменениях условий его реализации.
